正态分布是指什么？正态分布的定理、定义、特征及应用

2023-12-09 10:34:38

正态分布是指什么

一、正态分布是指什么

正态分布（英文：Normal distribution）又称为常态分布或高斯分布（Gaussian distribution），最早由棣莫弗（Abraham de Moivre）在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。

正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。

若随机变量X服从一个数学期望为μ、方差为σ2的正态分布，记为N(μ，σ2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

二、正态分布的发展

正态分布概念是由法国数学家棣莫弗（Abraham de Moivre）于1733年首次提出的，后由德国数学家Gauss率先将其应用于天文学研究，故正态分布又叫高斯分布，高斯这项工作对后世的影响极大，他使正态分布同时有了"高斯分布"的名称，后世之所以多将最小二乘法的发明权归之于他，也是出于这一工作。 [1] 但德国10马克的印有高斯头像的钞票，其上还印有正态分布的密度曲线。这传达了一种想法：在高斯的一切科学贡献中，其对人类文明影响最大者，就是这一项。在高斯刚作出这个发现之初，也许人们还只能从其理论的简化上来评价其优越性，其全部影响还不能充分看出来。这要到20世纪正态小样本理论充分发展起来以后。拉普拉斯很快得知高斯的工作，并马上将其与他发现的中心极限定理联系起来，为此，他在即将发表的一篇文章（发表于1810年）上加上了一点补充，指出如若误差可看成许多量的叠加，根据他的中心极限定理，误差理应有高斯分布。这是历史上第一次提到所谓"元误差学说"——误差是由大量的、由种种原因产生的元误差叠加而成。后来到1837年，海根（G.Hagen）在一篇论文中正式提出了这个学说。

其实，他提出的形式有相当大的局限性：海根把误差设想成个数很多的、独立同分布的"元误差" 之和，每只取两值，其概率都是1/2，由此出发，按棣莫弗的中心极限定理，立即就得出误差（近似地）服从正态分布。拉普拉斯所指出的这一点有重大的意义，在于他给误差的正态理论一个更自然合理、更令人信服的解释。因为，高斯的说法有一点循环论证的气味：由于算术平均是优良的，推出误差必须服从正态分布；反过来，由后一结论又推出算术平均及最小二乘估计的优良性，故必须认定这二者之一（算术平均的优良性，误差的正态性）为出发点。但算术平均到底并没有自行成立的理由，以它作为理论中一个预设的出发点，终觉有其不足之处。拉普拉斯的理论把这断裂的一环连接起来，使之成为一个和谐的整体，实有着极重大的意义。

三、正态分布的定理

由于一般的正态总体其图像不一定关于y轴对称，对于任一正态总体，其取值小于x的概率。只要会用它求正态总体在某个特定区间的概率即可。

为了便于描述和应用，常将正态变量作数据转换。将一般正态分布转化成标准正态分布。

若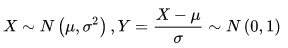标准正态分布

服从标准正态分布,通过查标准正态分布表就可以直接计算出原正态分布的概率值。故该变换被称为标准化变换。（标准正态分布表：标准正态分布表中列出了标准正态曲线下从-∞到X（当前值）范围内的面积比例。）

四、正态分布的定义

1、一维正态分布

若随机变量服从一个位置参数为、尺度参数为的概率分布，且其概率密度函数为：

正态随机变量

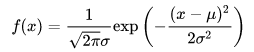
则这个随机变量就称为正态随机变量，正态随机变量服从的分布就称为正态分布，记作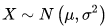正态分布01 ，读作X服从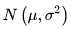正态分布02 ，或X服从正态分布。

μ维随机向量具有类似的概率规律时，称此随机向量遵从多维正态分布。多元正态分布有很好的性质，例如，多元正态分布的边缘分布仍为正态分布，它经任何线性变换得到的随机向量仍为多维正态分布，特别它的线性组合为一元正态分布。

本词条的正态分布是一维正态分布，此外多维正态分布参见"二维正态分布"。

2、标准正态分布

当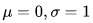正态分布03 时，正态分布就成为标准正态分布：

正态分布04

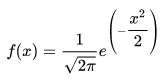
五、正态分布的特征

1、集中性：正态曲线的高峰位于正中央，即均数所在的位置。

2、对称性：正态曲线以均数为中心，左右对称，曲线两端永远不与横轴相交。

3、均匀变动性：正态曲线由均数所在处开始，分别向左右两侧逐渐均匀下降。

4、正态分布有两个参数，即均数μ和标准差σ，可记作N（μ，σ）：均数μ决定正态曲线的中心位置；标准差σ决定正态曲线的陡峭或扁平程度。σ越小，曲线越陡峭；σ越大，曲线越扁平。

5、u变换：为了便于描述和应用，常将正态变量作数据转换。

六、正态分布的应用

1、综述

(1)、估计频数分布一个服从正态分布的变量只要知道其均数与标准差就可根据公式即可估计任意取值范围内频数比例。

(2)、制定参考值范围

● 正态分布法适用于服从正态（或近似正态）分布指标以及可以通过转换后服从正态分布的指标。

●百分位数法常用于偏态分布的指标。表3-1中两种方法的单双侧界值都应熟练掌握。

(3)、质量控制：为了控制实验中的测量（或实验）误差，常以作为上、下警戒值，以作为上、下控制值。这样做的依据是：正常情况下测量（或实验）误差服从正态分布。

(4)、正态分布是许多统计方法的理论基础。检验、方差分析、相关和回归分析等多种统计方法均要求分析的指标服从正态分布。许多统计方法虽然不要求分析指标服从正态分布，但相应的统计量在大样本时近似正态分布，因而大样本时这些统计推断方法也是以正态分布为理论基础的。

2、频数分布

例1.10 某地1993年抽样调查了100名18岁男大学生身高（cm），其均数=172.70cm，标准差s=4.01cm，①估计该地18岁男大学生身高在168cm以下者占该地18岁男大学生总数的百分数；②分别求X+-1s、X+-1.96s、X+-2.58s范围内18岁男大学生占该地18岁男大学生总数的实际百分数，并与理论百分数比较。

本例，μ、σ未知但样本含量n较大，按式（3.1）用样本均数X和标准差S分别代替μ和σ，求得u值，u=（168-172.70）/4.01=-1.17。查附表标准正态曲线下的面积，在表的左侧找到-1.1，表的上方找到0.07，两者相交处为0.1210=12.10%。该地18岁男大学生身高在168cm以下者，约占总数12.10%。其它计算结果见表3。

表3 100名18岁男大学生身高的实际分布与理论分布

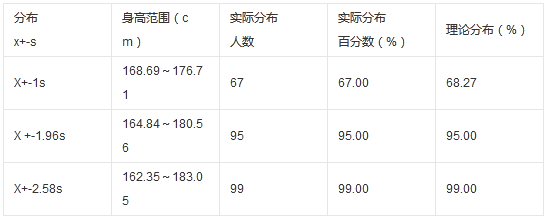
100名18岁男大学生身高的实际分布与理论分布

3、综合素质研究

教育统计学统计规律表明，学生的智力水平，包括学习能力，实际动手能力等呈正态分布。因而正常的考试成绩分布应基本服从正态分布。考试分析要求绘制出学生成绩分布的直方图，以"中间高、两头低"来衡量成绩符合正态分布的程度。其评价标准认为：考生成绩分布情况直方图，基本呈正态曲线状，属于好，如果略呈正（负）态状，属于中等，如果呈严重偏态或无规律，就是差的。

从概率统计规律看，"正常的考试成绩分布应基本服从正态分布"是正确的。但是必须考虑人与物的本质不同，以及教育的有所作为可以使"随机"受到干预，用曲线或直方图的形状来评价考试成绩就有失偏颇。许多教育专家（如上海顾泠沅、美国布鲁姆等）已经通过实践论证，教育是可以大有作为的，可以做到大多数学生及格，而且多数学生可以得高分，考试成绩曲线是偏正态分布的。但是长期受到"中间高、两头低"标准的影响，限制了教师的作为，抑制了多数学生能够学好的信心。这是很大的误会。通常正态曲线有一条对称轴。当某个分数（或分数段）的考生人数最多时，对应曲线的最高点，是曲线的顶点。该分数值在横轴上的对应点与顶点连接的线段就是该正态曲线的对称轴。考生人数最多的值是峰值。我们注意到，成绩曲线或直方图实际上很少对称的，称之为峰线更合适。

4、医学参考值

某些医学现象，如同质群体的身高、红细胞数、血红蛋白量，以及实验中的随机误差，呈现为正态或近似正态分布；有些指标（变量）虽服从偏态分布，但经数据转换后的新变量可服从正态或近似正态分布，可按正态分布规律处理。其中经对数转换后服从正态分布的指标，被称为服从对数正态分布。

医学参考值范围亦称医学正常值范围。它是指所谓"正常人"的解剖、生理、生化等指标的波动范围。制定正常值范围时，首先要确定一批样本含量足够大的"正常人"，所谓"正常人"不是指"健康人"，而是指排除了影响所研究指标的疾病和有关因素的同质人群；其次需根据研究目的和使用要求选定适当的百分界值，如80%，90%，95%和99%，常用95%；根据指标的实际用途确定单侧或双侧界值，如白细胞计数过高过低皆属不正常须确定双侧界值，又如肝功中转氨酶过高属不正常须确定单侧上界，肺活量过低属不正常须确定单侧下界。另外，还要根据资料的分布特点，选用恰当的计算方法。常用方法有：

(1)、正态分布法：适用于正态或近似正态分布的资料。

双侧界值：X+-u（u）S单侧上界：X+u（u）S，或单侧下界：X-u（u）S

(2)、对数正态分布法：适用于对数正态分布资料。

双侧界值：lg-1[X（lgx）+-u（u）S（lgx）]；单侧上界：lg-1[X（lgx）+u（u）S（lgx）]，或单侧下界：lg-1[X（lgx）-u（u）S（lgx）]。

常用u值可根据要求由表4查出。

(3)、百分位数法：常用于偏态分布资料以及资料中一端或两端无确切数值的资料。

双侧界值：P2.5和P97.5；单侧上界：P95，或单侧下界：P5。

表4常用u值表

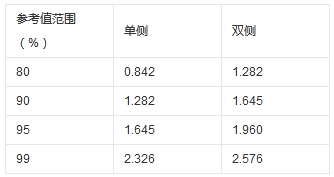
常用u值表

统计的理论基础：

如t分布、F分布、分布都是在正态分布的基础上推导出来的，u检验也是以正态分布为基础的。此外，t分布、二项分布、Poisson分布的极限为正态分布，在一定条件下，可以按正态分布原理来处理。

5、员工绩效

大部分员工的业绩，都是一般的，做得特别好的非常少，做得特别差的也不多见。这就是为什么绩效管理领域，会用"活力曲线"来考核业绩。

什么是"活力曲线"呢？

员工流失率太高显然不好。据计算，招聘的过程花费，大概是这名员工年薪的50％。过高的员工流失率，意味着失控的招聘成本。离职的业绩损失，大概是这名员工年薪的30%-400%。过高的员工流失率，更意味着巨大的业绩损失。

员工流失率太低也不好。极低的员工流失率，通常来自对低绩效的容忍。允许绩效差的员工留在团队，损失的不仅是工资，而是本应获得的业绩。另外，绩效差的员工通常更不愿离开，因为他可能找不到另一份工作。为了安全，他会想办法挤走绩效好的人，你的团队会越来越没有战斗力。

通用电气前CEO杰克·韦尔奇认为，大家很容易认识到员工流失率太高的问题，却很难认识到流失率太低的危害，所以，他提出了著名的"末位淘汰制"（也叫"活力曲线"），他把员工分为：

20%的优秀员工，70%的中等员工，和10%的末位员工。末位员工必须提升自己，或者转岗，或者面临淘汰。

这个制度，被认为是给通用电气带来无限活力的法宝之一。

所以，以后上班别偷懒，小心被老板裁掉。害怕吧？

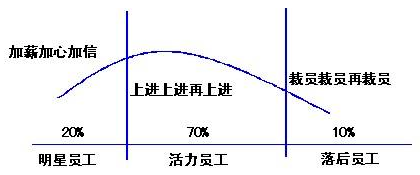
符合正态分布的商业现象

七、数据正态分布检验 Q-Q图

要观察某一属性的一组数据是否符合正态分布，可以有两种方法（目前我知道这两种，并且这两种方法只是直观观察，不是定量的正态分布检验）：

1：在spss(Statistical Package for the Social Sciences，即"社会科学统计软件包")里的基本统计分析功能里的频数统计功能里有对某个变量各个观测值的频数直方图中可以选择绘制正态曲线。具体如下：Analyze-----Descriptive Statistics-----Frequencies，打开频数统计对话框，在Statistics里可以选择获得各种描述性的统计量，如：均值、方差、分位数、峰度、标准差等各种描述性统计量。在Charts里可以选择显示的图形类型，其中Histograms选项为柱状图也就是我们说的直方图，同时可以选择是否绘制该组数据的正态曲线（With norma curve），这样我们可以直观观察该组数据是否大致符合正态分布。如下图：

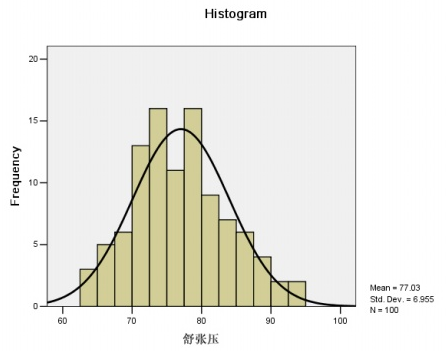
正态分布图

从上图中可以看出，该组数据基本符合正态分布。

2：正态分布的Q-Q图：在spss里的基本统计分析功能里的探索性分析里面可以通过观察数据的q-q图来判断数据是否服从正态分布。

具体步骤如下：Analyze-----Descriptive Statistics-----Explore打开对话框，选择Plots选项，选择Normality plots with tests选项，可以绘制该组数据的q-q图。图的横坐标为改变量的观测值，纵坐标为分位数。若该组数据服从正态分布，则图中的点应该靠近图中直线。

纵坐标为分位数，是根据分布函数公式F(x)=i/n+1得出的.i为把一组数从小到大排序后第i个数据的位置，n为样本容量。若该数组服从正态分布则其q-q图应该与理论的q-q图（也就是图中的直线）基本符合。对于理论的标准正态分布，其q-q图为y=x直线。非标准正态分布的斜率为样本标准差，截距为样本均值。

如下图：

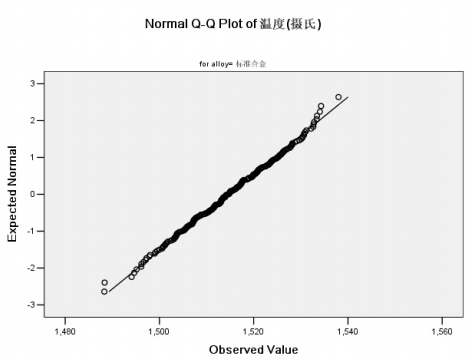
spss正态分布Q-Q图